While their effects are exquisitely described mathematically, fields are not given any physical consistency in physics; by contrast they occur in various dynamic formats of motion-activities in gravimotion. Protons when gathered form a mound dense in motion or acclivity called electrical field. Similarly electrons produce declivity type fields. An example of a strong electric field occurs in summer clouds in which electrons gather in quantity; the field gets so strong it creates its own paths to ground; the electrons travel through such paths in lightings, and that evens out the situation. This is another example of the equalization phenomenon (§1.4) at work.
While a number of protons or electrons create electrical fields, these electrical fields in return have an effect on individual protons and electrons.
And because fields and particles have identical constitution they are represented with similar density graphs; fields have larger magnitudes and densities than those of individual particles.
The 4 combinations protons, electron within acclivity declivity are illustrated as follows:
Hover figure 5.1.1 with the computer's mouse pointer.
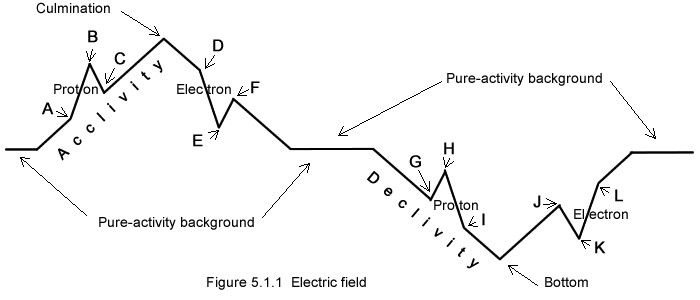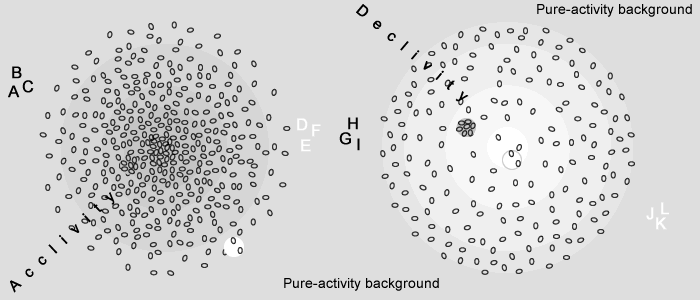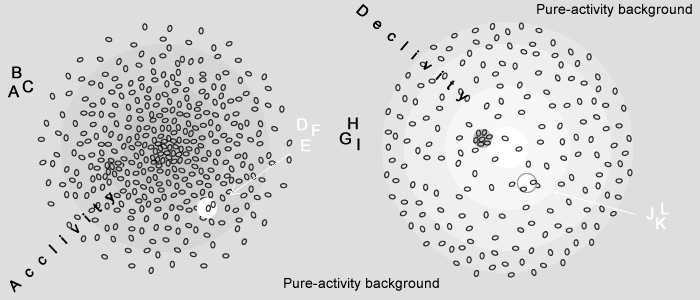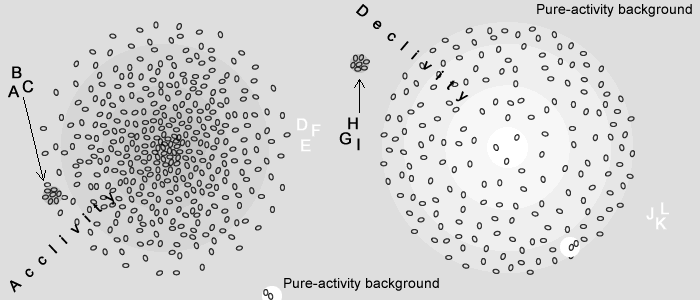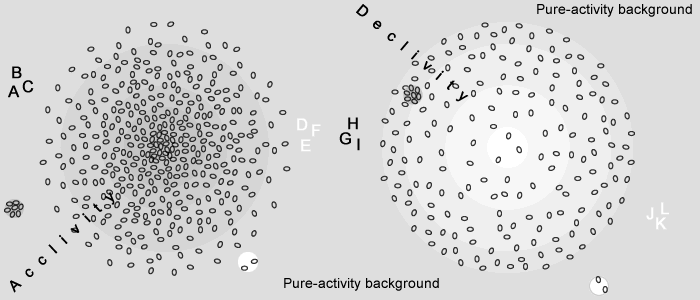The proton "ABC" is "squeezed out" and away from the acclivity (positive field) on the left.
The electron "DEF" is "sucked into" and toward the center of the same acclivity graded activity.
The proton "GHI" is "squeezed toward" the center of the declivity type graded activity on the right.
The electron "JKL" is "sucked out" and away from the same declivity.
One must keep in mind that while electric fields acclivity and declivity are occurring as gradient of great numbers of protons and electrons, protons and electrons themselves are occurring as great numbers of motion-occurrences; in the end fields and particles are occurring under MOs amd MQs (all under the same stuff), the whole operations being homogeneous.
For simplicity and easier comprehension, the animated illustration background (the pure-activity) has been represented with a grey color rather than with Maxwellian MQs. In the same spirit the acclivity is getting darker in the center, while the declivity (negative field) is getting lighter toward the center. Similarly the protons are darker than the electrons.
The integrity of electrical fields and particles is maintained through various internal and external factors. As such particles do not dissolve in a field’s acclivity or declivity. On the other hand protons and electrons modify the local landscape of a field, which in return partially modifies the particles motion and constitution, as motion and constitution of a particle make one.
Protons and electrons in a graded environment end up out of equilibrium. They become lame particles within an electrical field.

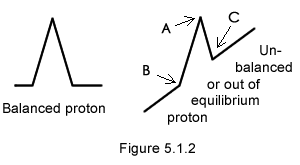
Let us consider the proton ABC represented on both figures 5.1.1 and 5.1.2.
The proton’s density being tipped sideways, the MOs forming it are out of equilibrium; they have a tendency to move away from the high density volume, following the density curve. While the field’s acclivity is increased at a new junction "B" it is restored to its original state in "C".
This can be summarized saying that the proton being out of equilibrium seeks equilibrium moving away from the acclivity background. It obeys the equalization phenomenon (§1.4).
Now let us consider the case of the electron "D, E, F" on the right side of the acclivity; the MOs along "D-E" move toward the lower concentration "E-F" yet being larger in number their motion will not stop until equilibrium is set. The electron ends up climbing the density curve.
The same mechanisms apply to the right side of the picture; in that case we find that a proton moves toward the bottom of a declivity made of electrons (negative field in physics) while electrons are repelled by the same; in short the motion of "H, I, G" is identical to that of "A, B, C".
All of this while not part of physics is nevertheless in accordance with the first of Maxwell famous 4 equations. The purpose of gravimotion is not to compete with physics mathematics; the purpose of gravimotion is to provide a qualitative interpretation of physics mathematics.
Gravimotion’s graded-activity merges both physics’ concepts of electric charge and electric field. Then it provides a physical illustration (figure 5.1.1) of the behavior of a particle within a so called divergent electrical field